Median and MAD Revisited with an Online Estimator

In a previous post a faster Selection algorithm was demonstrated. This will be revisited focusing on the Median and MAD statistical measures and their practical use in performance testing.

Though the Median is robust to outliers and a very useful measure, one downside is it requires all the sample values to be kept for the calculation. For online algorithms as the sample size increases this creates a memory problem. An online algorithm will be provided to estimate the Median and MAD in fixed memory.

Exact Median Algorithm

This algorithm is based on the MODIFIND algorithm by Vladimir Zabrodsky. In the previous post it was shown to behave well with partially sorted and duplicate data.

module Statistics =
    let medianInPlace (a:float[]) (index:int) (length:int) =
        let inline swap (a:float[]) i j =
            let temp = a.[i]
            a.[i]<-a.[j]
            a.[j]<-temp
        let inline swapIf (a:float[]) i j =
            let ai = a.[i]
            let aj = a.[j]
            if ai>aj then
                a.[i]<-aj
                a.[j]<-ai
        let k = length >>> 1
        let rec outerLoop lo hi =
            swapIf a lo k
            swapIf a lo hi
            swapIf a k hi
            let pivot = a.[k]
            let resetLo = if a.[lo]=pivot then a.[lo]<-Double.MinValue; true else false
            let resetHi = if a.[hi]=pivot then a.[hi]<-Double.MaxValue; true else false
            let mutable i = lo+1
            let mutable j = hi-1
            while a.[i]<=pivot do i<-i+1
            while a.[j]>=pivot do j<-j-1
            while i<k && k<j do
                swap a i j
                i<-i+1
                j<-j-1
                while a.[i]<=pivot do i<-i+1
                while a.[j]>=pivot do j<-j-1
            if i<j then
                swap a i j
                if k<j then
                    i<-lo
                    j<-j-1
                    while a.[j]>=pivot do j<-j-1
                else
                    j<-hi
                    i<-i+1
                    while a.[i]<=pivot do i<-i+1
            else
                if k<j then i<-lo
                elif k>i then j<-hi
            if resetLo then a.[lo]<-pivot
            if resetHi then a.[hi]<-pivot
            if i>=j then
                if length &&& 1 = 0 && j+1=k then
                    let mutable v = a.[lo]
                    for i = lo+1 to j do
                        if a.[i]>v then v<-a.[i]
                    (v + pivot) * 0.5
                else pivot
            else outerLoop i j
        outerLoop index (index+length-1)

Performance Testing

The algorithm is compared to a full sort, the Math.Net Quickselect and the Perfolizer QuickSelectAdaptive algorithms.

This performance testing technique created as part of a new testing library prototype uses a statistical test on the counts of the faster of two algorithms. The Median and MAD are estimated as useful information. As well as being robust to outliers they are also a good compliment since the faster algorithm will always have a positive Median performance improvement. This may not be true of the Mean.

Performance testing can be run across all threads and also while running other tests. It is also able to compare a range of input data instead of just a single data input.

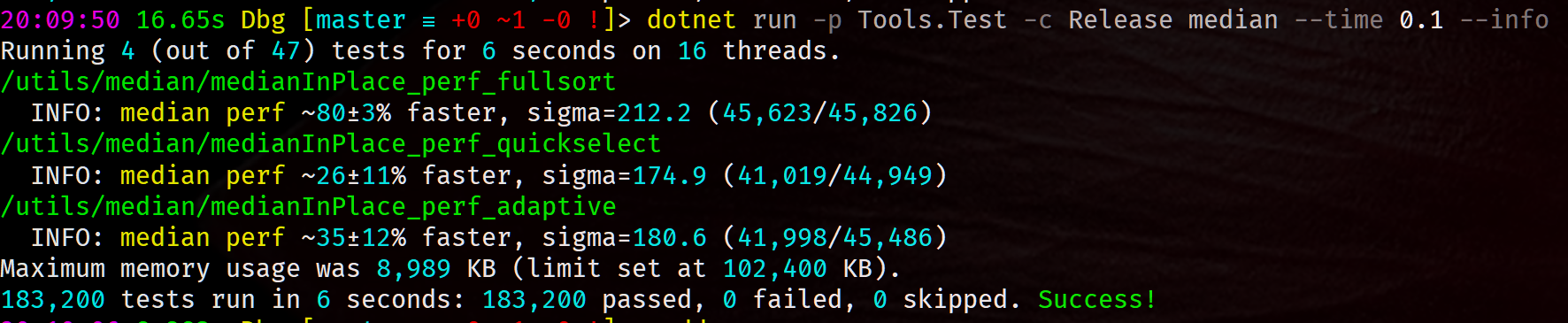
It reaches statistically significate results extremely quickly compared to tests based on the Mean. A sigma of 6 gives a good stopping criteria and is used when skipping completed tests.

Online Estimator

In a previous post online statistical calculations were discussed. The following online Median and MAD estimator is a hybrid of an exact Median and MAD calculation followed by a recursive estimator. The size of the exact sample N and a learning rate Eta are taken as a parameters.

The standard error of the sample Median approximates to:

\[SE \sim \frac{MAD}{\sqrt{n}}\]

A fixed fraction Eta of the MAD for the learning rate is used as it provides a parameter with a sensible scale.

type MedianEstimator =
    val mutable private A : float array
    val mutable private Median : float
    val mutable private MAD : float
    val private Eta : float
    val mutable N : int
    new(n:int,eta:float) =
        {A = Array.zeroCreate n; Median = 0.0; MAD = 0.0; Eta = eta; N = 0}
    member m.MedianAndMAD =
        if isNull m.A then m.Median, m.MAD
        else
            let median = Statistics.medianInPlace m.A 0 m.N
            let mad = Array.sub m.A 0 m.N
            for i = 0 to mad.Length-1 do
                mad.[i] <- abs(mad.[i]-median)
            median, Statistics.medianInPlace mad 0 mad.Length
    member m.Add (s:float) =
        if isNull m.A then
            m.Median <- m.Median +  m.MAD * m.Eta * float(sign(s-m.Median))
            m.MAD <- m.MAD +  m.MAD * m.Eta * float(sign(abs(s-m.Median)-m.MAD))
            m.N <- m.N + 1
        else
            m.A.[m.N] <- s
            m.N <- m.N + 1
            if m.N = m.A.Length then
                let median, mad = m.MedianAndMAD
                m.Median <- median
                m.MAD <- mad
                m.A <- null

For performance testing N=99 and F=0.001 give stable results.

Conclusion

The superior performance of the MODIFIND algorithm has again been demonstrated compared to current algorithms.

A new type of statistical performance testing has been introduced with useful features of being able to run in parallel and across a range of inputs efficiently.

A fixed memory online Median and MAD estimator has been created to provide efficient and consistent statistics for use in performance testing and other performance critical applications.

Although early days these techniques together look to provide robust and efficient results.