Statistic Estimators

01 Nov 2021

The following are a family of fixed low memory, high performance statistic estimators.

• Moment4Estimator - Mean, Standard Deviation, Skewness and Kurtosis unbiased estimator.
• Moment3Estimator - Mean, Standard Deviation and Skewness unbiased estimator.
• Moment2Estimator - Mean and Standard Deviation unbiased estimator.
• Moment1Estimator - Mean estimator.
• QuantileEstimator - Single quantile p estimator using min, p/2, p, (1+p)/2, max estimation points.
• QuartileEstimator - Median, Min, Max, Lower Quartile and Upper Quartile estimator. This is the data required to produce a box plot.
• QuantilesEstimator - Multiple quantile estimator with min and max points.
• HistogramEstimator - Histogram estimator by equal quantile range bucketing.

They can incrementally add observations and statistics can be calculated at any point. All have an Add and + operator overload to combined the summary statistics from two separate estimators. They are self contained classes that can be copied easily.

Moment Estimators

The moment estimators are a performance optimised set of unbiased central and standard moment calculations. The algorithms used are detailed here. Nothing radical just performance optimised code to the specific statistics required.

P² paper

This paper by Dr Raj Jain and Dr Imrich Chlamtac describes a great way to estimate ordered statistics like median and quantiles without storing all the observations. The remaining estimators are based on this paper.

Unfortunately there are some problems with the algorithms put forward in the paper which need correcting:

1. The marker increments added each iteration create a rounding error which is important since the marker is compared to integer counts.
2. The inequality operators used on the quantile values do not agree with the definition of the cumulative distribution function.
3. The Piecewise-Parabolic (P²) interpolation used can produce poor results as the fitted quadratic is not monotonic.

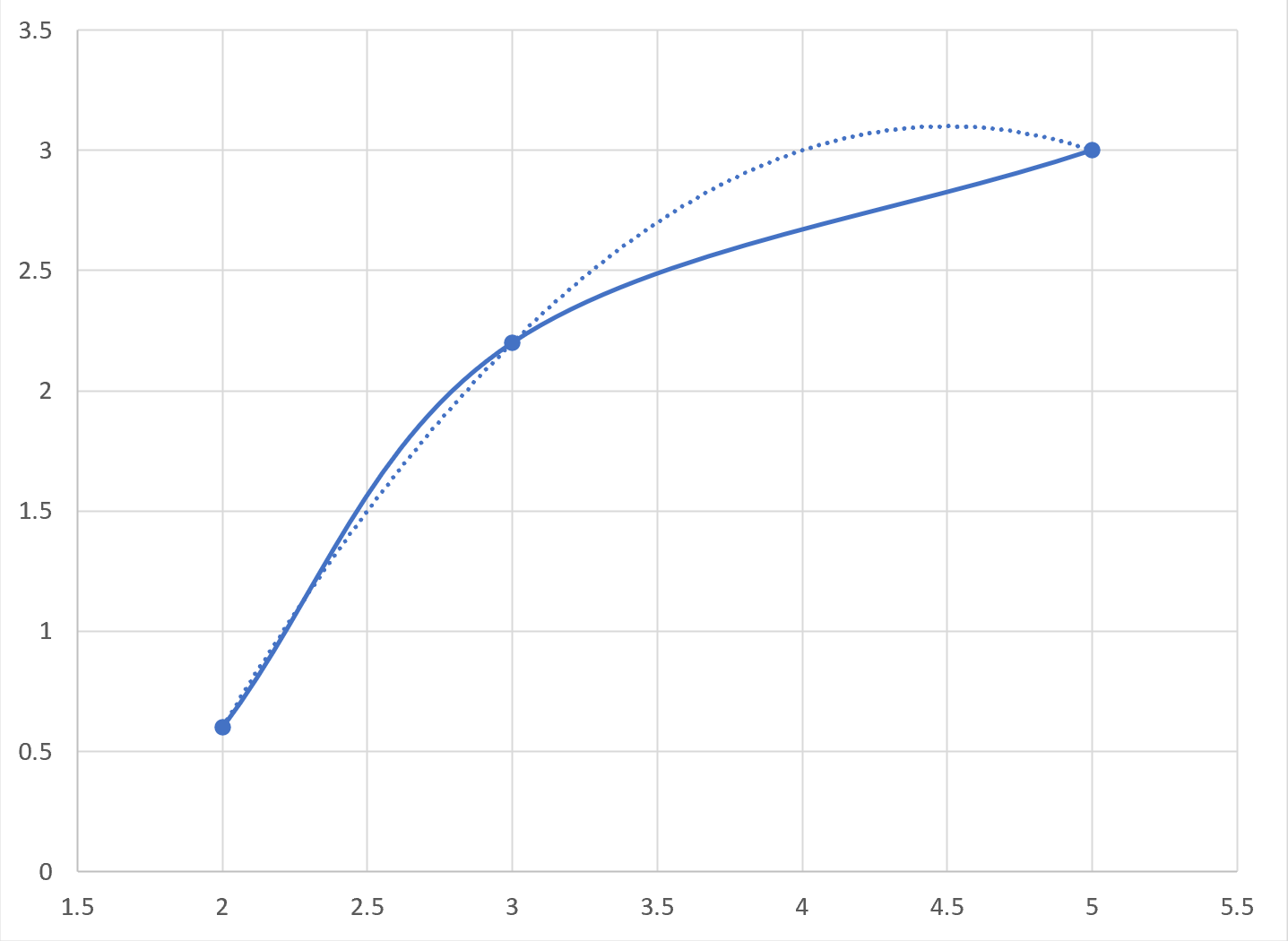
Here the dotted line is the fitted quadratic around the middle point that needs to move from 3 to 4.

To correct 1. we cannot use increments and need to just calculate the desired marker position. Increments were suggested to reduce CPU overhead, but from performance testing in .NET this is not the case.

To correct 2. we need to compare if the observations are less than or equal to the quantile value as per the CDF definition. We also need to allow the possibility that there are more than one observation of the minimum value. Some distributions can produce duplicate values and also a large number of the minimum value.

To correct 3. we need to replace the interpolation. The issue is not that the quadratic can overshoot since the algorithm checks this and falls back to linear interpolation. The problem is that it can produce results that are arbitrarily close to one of the points it is next to.

PCHIP interpolation

Fortunately there is a monotonic interpolation function that works well and is quick to calculate.

PCHIP, or harmonic spline, is a cubic spline interpolation algorithm. It has been implemented in a number of places such as SciPy and MathNet.

PCHIP is very useful for modelling yield curves as it produces a visually pleasing, stable local interpolation.

For the estimators the PCHIP interpolation actually simplifies as the movement is always by one which removes some terms from the calculation, and the data always has increasing (and not equal) x and y values which removes some testing and branching.

Conclusion

The memory requirement for these estimators is small and fixed, regardless of the number of observations.

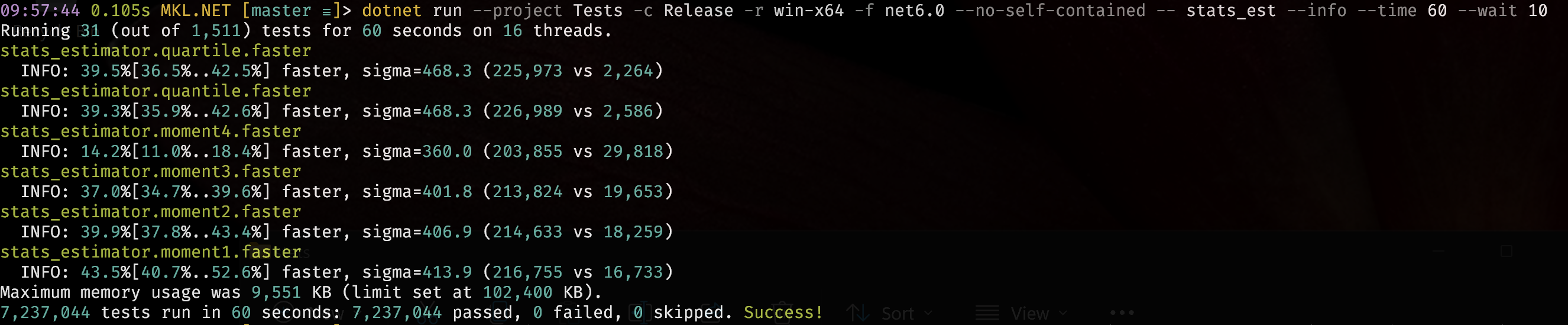
Performance has been optimised with QuartileEstimator being around 40% faster than other more faithful implementations.

The efficiency and low memory of these estimators makes them useful for a wide range of uses from performance measurement as above to monitoring and telemetry more generally.

Here are the code and tests.