A robust weighted allocation algorithm thanks to CsCheck
14 Sep 2022Allocating an integer total over a set of weights is surprisingly tricky. Consider a poll result where round percentages are required to add up to 100. Or money or shares to be allocated to a number of accounts.
The most common way of solving this is to round the results and then adjust the largest weights for any residual difference.
This can produce nonsensical results. It can lead to larger weights getting a smaller allocation. For small totals it can result in the largest weight getting no allocation at all.
With the help of CsCheck we will revisit this algorithm.
CsCheck
We can create random tests to check for these kinds of issues. They guide us to the simplest algorithm that satisfy the requirements. The random test code not only gives us many simple failing examples, but also hints at the solution.
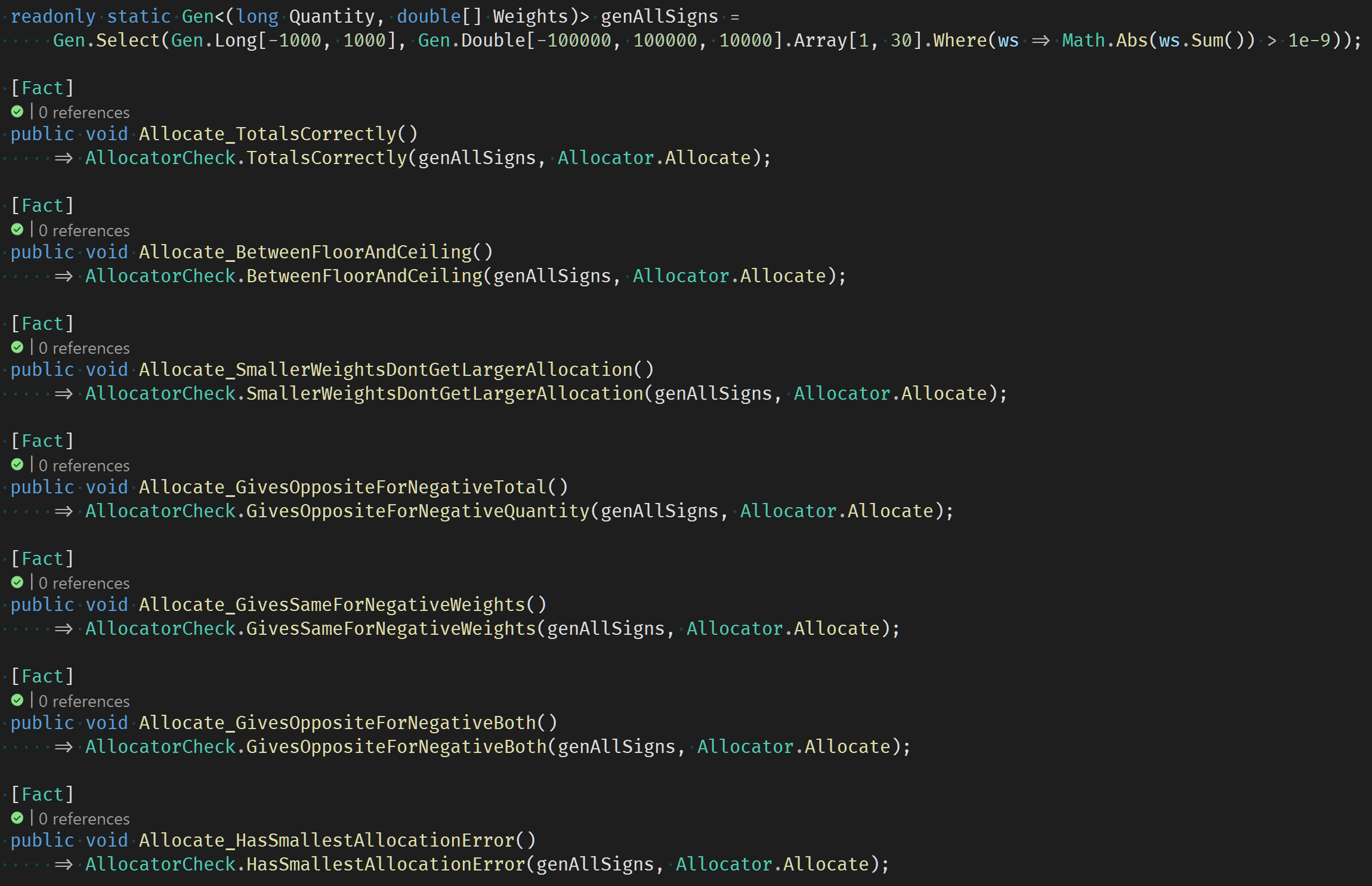
Error Minimising Algorithm
In this case the solution is an error minimisation algorithm, which then guarantees smaller weights never get larger allocations.
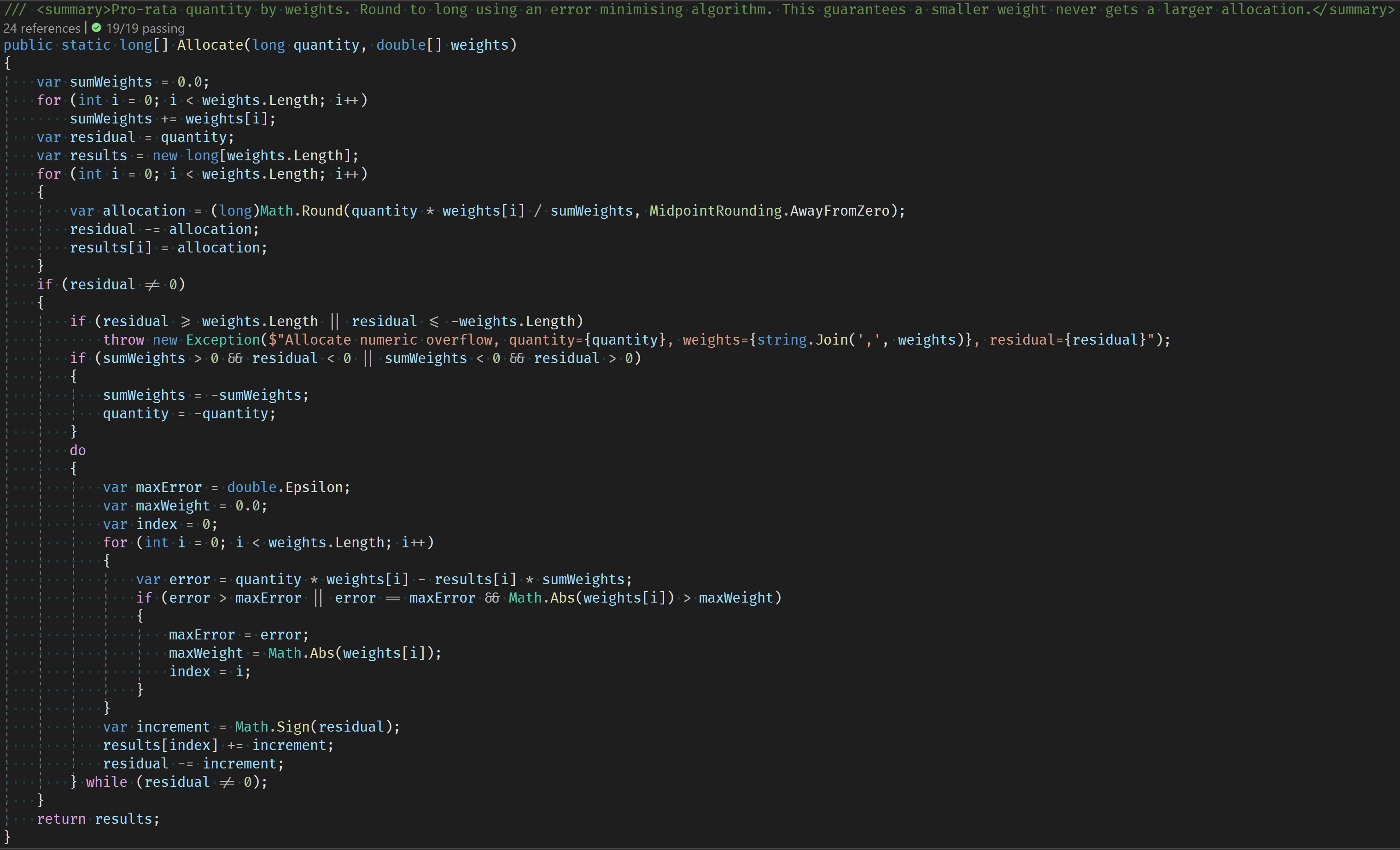
Conclusion
Writing random tests leads to a robust algorithm that covers all possible inputs including negative values.
There were also some nasty precision rounding issues to solve that would be hard to spot using standard unit testing and a handful of examples.

