Balinski-Young weighted allocation algorithm
31 Oct 2022We will cover an alternative weighted allocation algorithm to the one in the previous post. These algorithms are used to allocate an integer total quantity over a set of weights.
Balinski and Young proved that no allocation algorithm can be free of perceived unintuitive observations, or paradoxes.
The algorithm in the previous post is the most fair with minimum error but it does suffer from the Alabama paradox. This is when for a small increment of the total quantity there can be a decrease in one of the allocated values.
Balinski-Young Algorithm
Balinski and Young constructed an algorithm that follows the quota rule (all values are either the floor or ceiling of the unrounded allocation) and is free of the Alabama paradox.
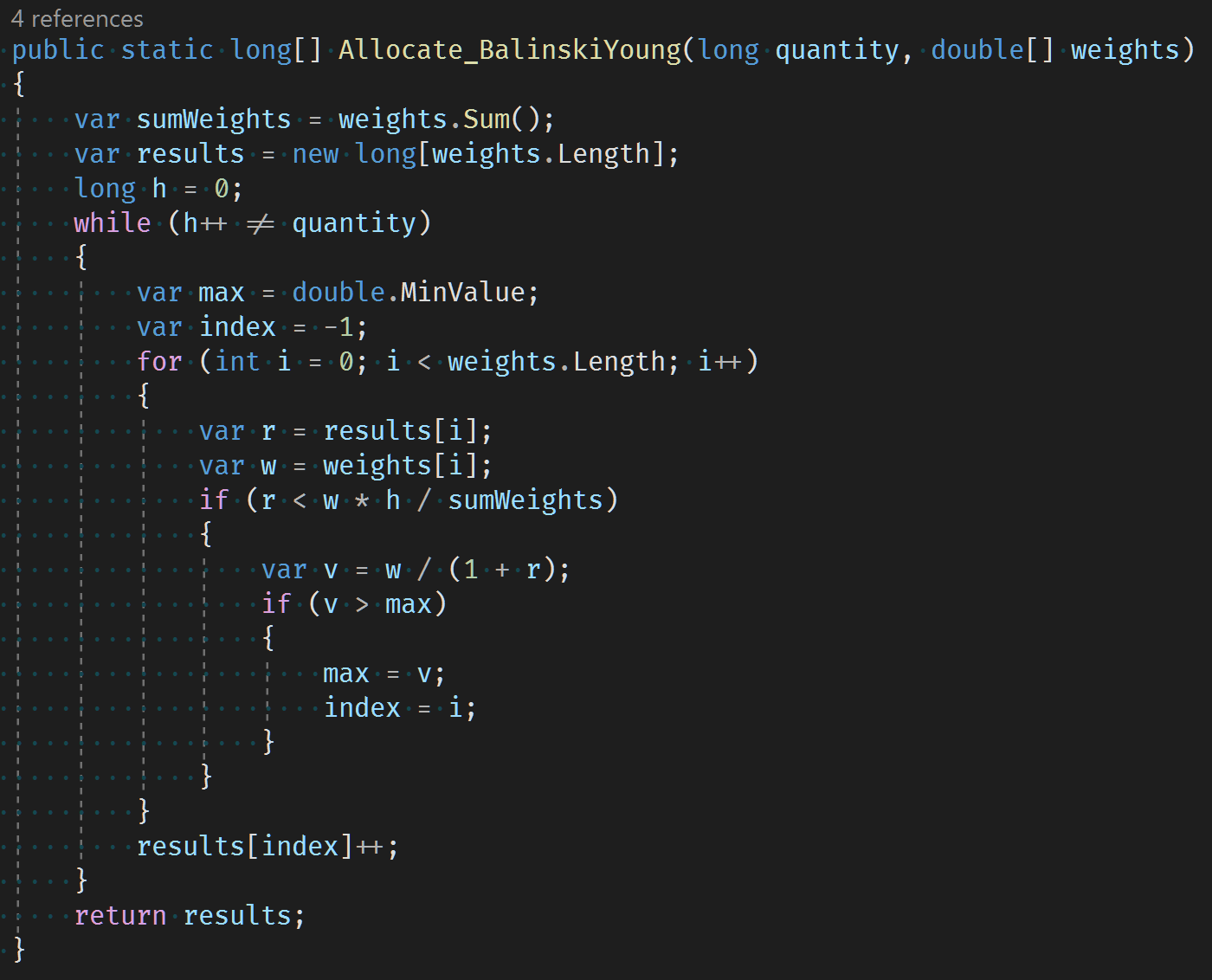
Again this is tested with CsCheck including a test for the Alabama paradox.
Conclusion
The Balinski-Young algorithm is said to be slightly biased towards larger weights. It can be useful in situations where there is the possibility of small incremental increases to the total quantity.
There is little online about this algorithm (or the one in the previous post) and many unanswered questions. From twitter polls not looking correct, to algorithms with poor properties such as cascade rounding or adjusting the largest weights, there seem to be common software errors in this area.

