An improved root-finding method

03 Jun 2021

This method uses two ways to reduce the number of functions calls needed for root-finding. The first is to create a hybrid of Brent's method and Muller's method. The second is to start with points inside the given boundary instead of evaluating the boundary straight away.

Hybrid

Brent's method is a hybrid root-finding algorithm combining inverse quadratic interpolation, linear interpolation and the bisection method. It has multiple conditions that are used to decide between the potentially fast-converging inverse quadratic interpolation or linear interpolation, or fall back to the more robust bisection method. These are quite tricky to correctly implement and most stick to standard sources such as "Algorithms for Minimization without Derivatives" by Richard Brent or "Numerical Recipes".

Muller's method uses quadratic interpolation recursively.

Our hybrid method combines quadratic interpolation, inverse quadratic interpolation and the bisection method (if either of the interpolations do not fall within the bound region then linear interpolation is used). Our condition for moving on to the next method is simply if the bound region is being reduced by less than 40%. If greater we return to the quadratic interpolation level. Bisection will always return to this level also. The rough logic of the algorithm is that generally quadratic is the most useful interpolation but if it under or over shoots then inverse quadratic could do the opposite and fix any problem with the convergence, falling back to bisection as Brent does.

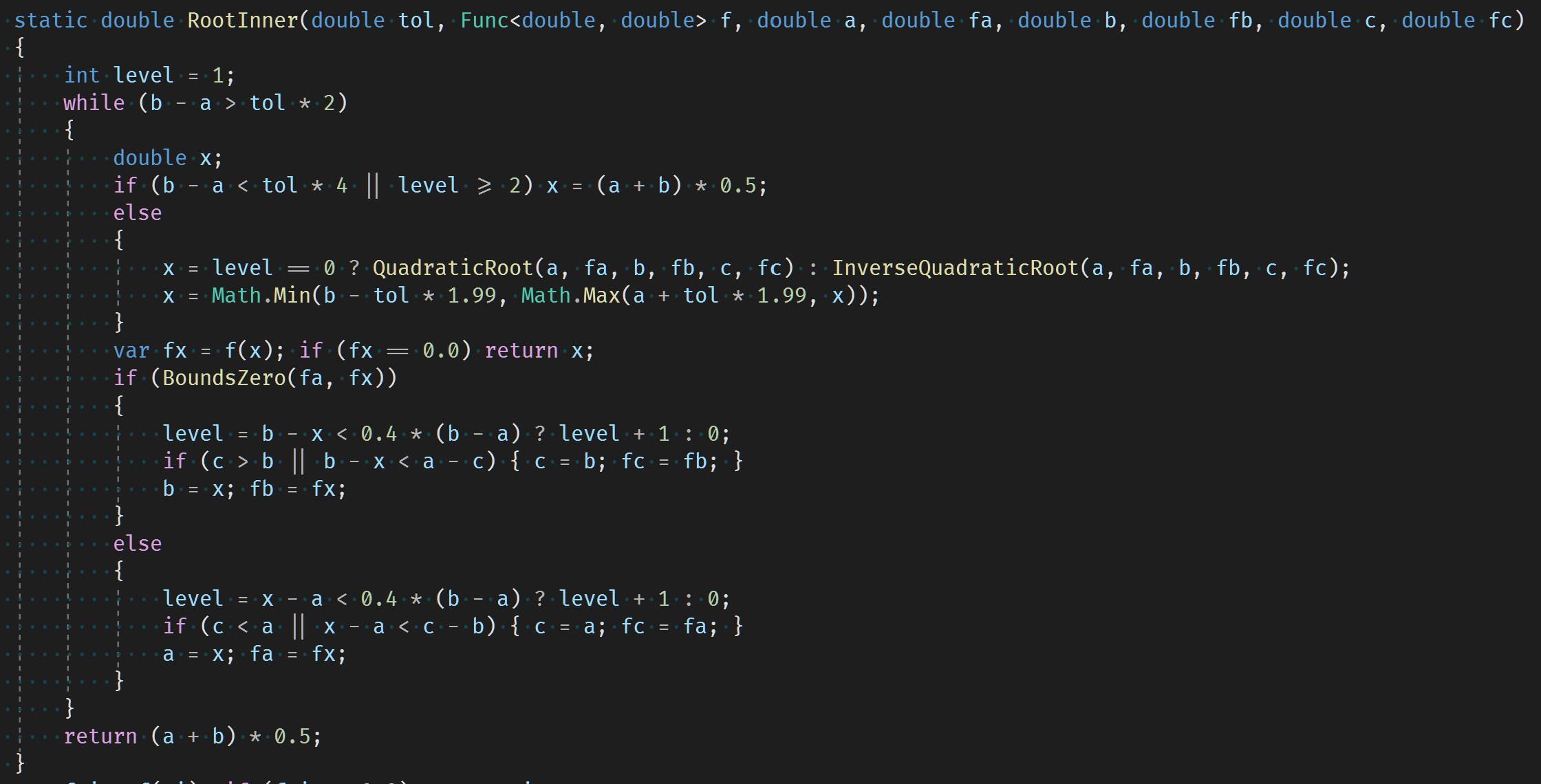
Boundary

Brent's method first evaluates the given boundary points.

Our method evaluates points 20% in from the boundary. If the root is bound by these points then we have successfully cut the bound region by 40%. If not then by looking at the function values we should have a good indication which of the 20% end regions to test. As a further optimisation our method uses linear interpolation to find a point estimate in these end regions and tests a point 20% further towards the boundary in the hope to bound the root in a much reduced region. Our method falls back to testing a boundary point if all this fails.

There is a balance between the size of the inner region and the boundary regions. Too close to boundary and the inner region is not so much of a win, and too far in and we likely end up evaluating the boundary with other wasted evaluations along the way.

20% was found to be about right from the test problems.

Numerical Results

The 154 test problems from Enclosing Zeros of Continuous Functions were used to compare the root-finding methods.

The total number of functions calls are:

Tol	Brent	Hybrid	Overall
1e-6	2763	2446	2144
1e-7	2816	2544	2237
1e-9	2889	2592	2292
1e-11	2935	2632	2329

Each of our improvements gives about a 10% reduction in the number of function calls resulting in an overall 20% improvement.

Our method was also tested on bond spread and option volatility problems which compare favourably to Brent.

Conclusion

The boundary improvement has been extended to allow the caller to set these inner evaluation points. This is very useful when you have a good idea of the area the solution should be in from say a previous calibration result. This additional reduction of calls for prior information is demonstrated in the bond spread and option volatility tests.

A 20% reduction in function calls is a great result but we must consider we may have overfitted to this problem set. The bond spread and option volatility give some comfort this result holds more generally but further testing on other problems is needed.

The code is easy to follow and it is obvious a solution will always be found. There may be further optimisations or features that can be added.

The code and tests can be found here.