Full precision floating-point summation in C#

Shewchuk proved that the following algorithm using multiple nonoverlapping partial sums exactly represents the sum of a sequence of floating-point values. The error in the returned sum of the partial sums is less than one ulp. This depends on IEEE-754 arithmetic guarantees.

TwoSum Algorithm

TwoSum is a floating-point algorithm for computing the exact round-off error in a floating-point addition operation where \(hi + lo = a + b\) exactly. The \(hi\) and \(lo\) values are nonoverlapping meaning the least significant nonzero bit of \(hi\) is more significant than the most significant nonzero bit of \(lo\).

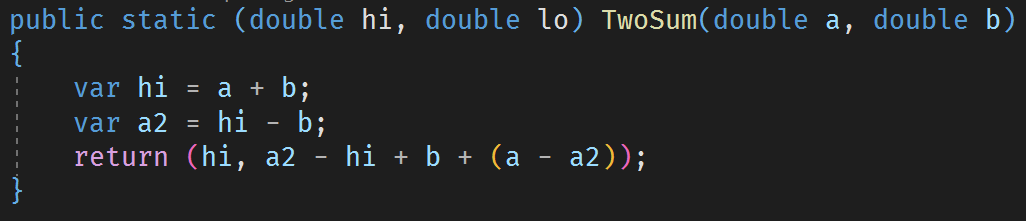
Shewchuk Algorithm

This algorithm tracks all the "lost digits" as the values are added so that the returned value only has a single rounding. The inner loop applies TwoSum hi/lo summation to each partial so that the list remains exact.

A good demonstration of this algorithm is FSum([1e100, 1, -1e100, 1e-100, 1e50, -1, -1e50]) = 1e-100.

The algorithm has been optimised for C# though remains a few times slower than a normal sum. Holding the hi and lo in variables reduces the number of times the partials span needs to be accessed.

Neumaier Algorithm

This algorithm is faster but without the full round-off error reduction.

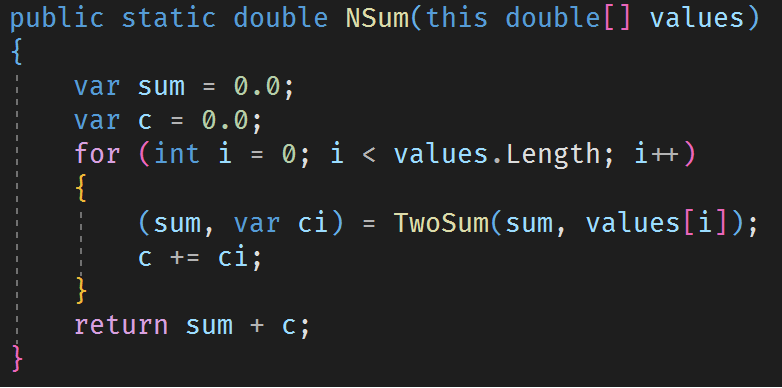
Conclusion

An optimized C# implementation of the Shewchuk algorithm for full precision summation has been developed, and also the faster but less accurate Neumaier algorithm. As always these have been comprehensively tested with CsCheck.

Python has a version of the Shewchuk algorithm as fsum in the math module of the standard library. In the recently released Python 3.12 the built-in sum function has been changed to use the Neumaier algorithm to reduce numerical error for a smaller performance penalty.

In an upcoming post FSum and NSum will be used to improve the error minimising allocation algorithm.

Links:
TwoSum
Adaptive Precision Floating-Point Arithmetic and Fast Robust Geometric Predicates
C# TwoSum, NSum and FSum
Python math.fsum
ASPN cookbook recipes for accurate floating point summation
Kahan and Neumaier summation algorithms